Array Statistics and Visualization
The Statistics dropdown of the Array View provides access to statistical information generated from the array values.
On this page:
Viewing Array Statistics
Figure 59. The Array Statistics view
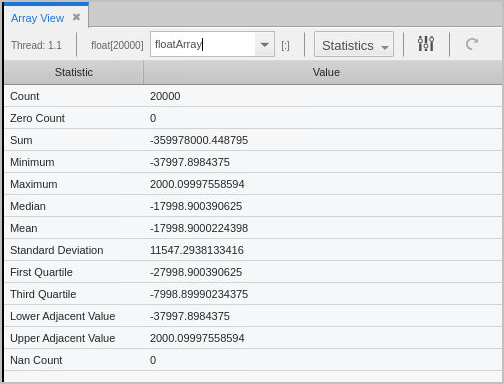
The above is a one-dimensional floating point array composed of 20,000 elements, identified under the Count statistic. See Array Statistics Detail for information on all displayed statistics.
Array statistics are also available through the CLI, as switches to the dprint command.
|
|
|
|
Cast a variable to an array |
|
|
Slicing array data |
|
|
Displaying arrays |
Array Statistics Detail
If you have added a slice (see Slicing Arrays), these statistics describe only the information currently being displayed; they do not describe the entire array. For example, if an array includes positive values, but a slice omits array values that are more than 0, the median value is negative even though the entire array’s real median value is more than 0.
Count
The total number of displayed array values. If you’re displaying a floating-point array, this number doesn’t include NaN or Infinity values.
Zero Count
The number of elements whose value is 0.
Sum
The sum of all the displayed array’s values.
Minimum
The smallest array value.
Maximum
The largest array value.
Median
The middle value. Half of the array’s values are less than the median, and half are greater than the median.
Mean
The average value of array elements.
Standard Deviation
The standard deviation for the array’s values.
Quartiles, First and Third
Either the 25th or 75th percentile values. The first quartile value means that 25% of the array’s values are less than this value and 75% are greater than this value. In contrast, the third quartile value means that 75% of the array’s values are less than this value and 25% are greater.
Lower Adjacent Value
This value provides an estimate of the lower limit of the distribution. Values below this limit are called outliers. The lower adjacent value is the first quartile value minus the value of 1.5 times the difference between the first and third quartiles.
Upper Adjacent Value
This value provides an estimate of the upper limit of the distribution. Values above this limit are called outliers. The upper adjacent value is the third quartile value plus the value of 1.5 times the difference between the first and third quartiles.
Denormalized Count
A count of the number of denormalized values found in a floating-point array. This includes both negative and positive denormalized values as defined in the IEEE floating-point standard. Unlike other floating-point statistics, these elements participate in the statistical calculations.
Infinity Count
A count of the number of infinity values found in a floating-point array. This includes both negative and positive infinity as defined in the IEEE floating-point standard. These elements do not participate in statistical calculations.
NaN Count
A count of the number of NaN (not a number) values found in a floating-point array. This includes both signaling and quiet NaNs as defined in the IEEE floating-point standard. These elements do not participate in statistical calculations.
Checksum
A checksum value for the array elements.
Visualizing Array Data
To visualize your data, choose either Histogram Plot, Line Plot, or Surface Plot from the Statistics dropdown.
Different datasets can require different views to display their data. For example, you could use a histogram to see the distribution of a dataset, or lines and surface plots to view trends or slope.
The examples here display all the data for an array. To display a subset, you can slice the data. See Slicing Arrays.
Histogram View
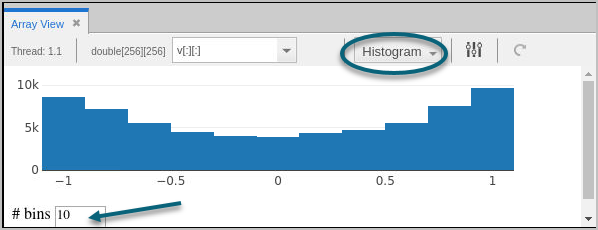
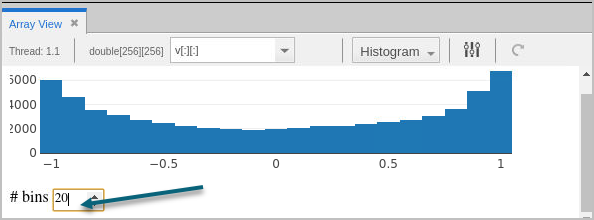
By default, the view displays 10 bins, or buckets:
|
|
|
|
Line Plot View
To display your data as x and y coordinate pairs, use the Line Plot view. This view is useful to plot trend lines in your one-dimensional datasets. For example:
Figure 61. Array Data > Line Plot
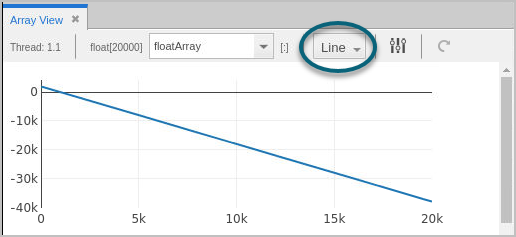
Note that for higher-dimensional datasets in the Array View, the Line Plot displays a flattened, one-dimensional dataset. For example, given an array like this:
[[31 12 43][42 1 16
[0 42 0]]
The Line Plot displays a flattened array, like so:
[31 12 43 42 1 16 0 42 0]
Surface Plot View
The Surface plot displays two-dimensional datasets as a surface in two or three dimensions. The dataset’s array indices map to the first two dimensions (X and Y axes) of the display, and the values map to the height (Z axis). This can be useful to show a relationship across three variables and to observe trends in two-dimensional datasets.
Figure 62. Array View: Surface Plot View
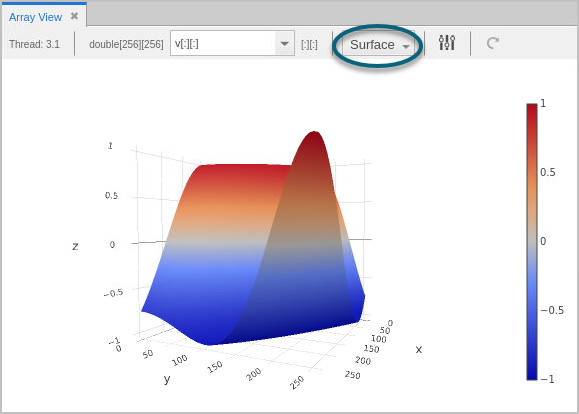
Use the plot controls to rotate or zoom the display.

Updating the View
After advancing your program, the view does not update automatically. To refresh the display, click the Update button (![]() ).
).
Changing the Thread of Focus
if you change the program’s thread of focus, it’s not reflected in the array displayed in the Array View, which displays the original thread of focus when the array was added to the view. You can, however, maintain multiple arrays in the Array View that are tied to different threads of focus.
Zooming Into Data
To view some data in detail, use the zoom toolbar, which displays when you place your cursor inside the graph:
To zoom in, either:
Use the Plus button ( ).
).
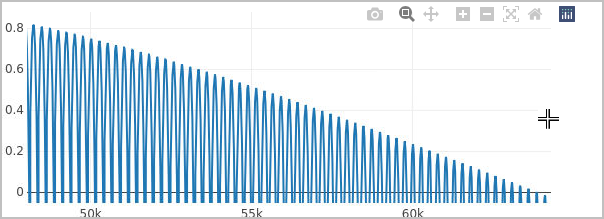
Drag an area to view:

TotalView zooms in on your data:
Figure 63. Array View > zooming in on data
To undo the zoom, either double-click on the graph or select the Reset Axes home button ( ) or the Zoom out button (
) or the Zoom out button ( ).
).
If you know the indices you want to examine, you can also slice the array to view a subsection; see Slicing Arrays.
|
|
|
|
Slicing arrays to visualize or see statistics for a subsection of an array |
|
|
Viewing arrays in the Data View |
|
|
Displaying arrays |